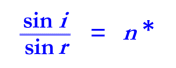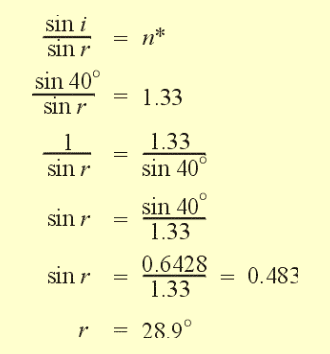You may have learned that the speed of light is constant (about 30
000 000 metres per second). In actual fact it is only constant if it is
travelling through a medium (material - eg. air) of constant density. When
light encounters an increase in density, it slows down. When light encounters
a decrease in density it speeds up. These changes in speed correspond to
changes in direction so changes in density cause the path of light to bend.
See below.

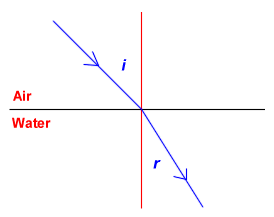
Air to Water
When light travels from air to water it slows down because water is more
dense than air is. When light slows down its path bends towards
the normal line so that the angle of incidence (i) is greater than
the angle of refraction (r), i >
r. Eg.
 |
 |
As light travels from air to water it is
bent towards the normal line, i.e. the
angle of incidence is greater than the
angle of refraction. |
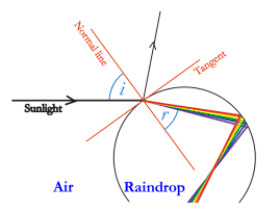
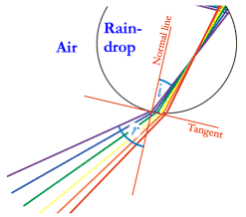
This also occurs in the formation of a rainbow. The normal line it
perpendicualr to the tangent at the point where the light hits the surface
of the raindrop. |
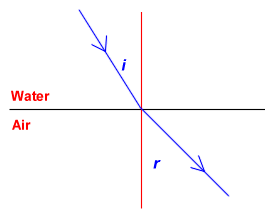
Water to Air
When light travels from air to water it slows down because water is more
dense than air is. When light slows down its path bends towards
the normal line so that the angle of incidence (i) is greater than
the angle of refraction (r), i >
r. Eg.
 |
 |
As light travels from air to water it is
bent towards the normal line, i.e. the
angle of incidence is less than the
angle of refraction. |
When light travels back out of the raindrop, the same thing occurs.
The diagram above shows the angles for
the violet ray. |
Refractive Index
It is possible to find the angles of incidence refraction by careful ray-tracing
and measurement. You may have tried this using a Hudson Light Box. This
method is time consuming and can be very inaccurate. For this reason scientists
in the 16th and 17th centuries devoted years to trying to find a mathematical
relationship to link the values of the angle of incidence and the angle
of refraction.
In 1621 Willebrord Snell, a Dutchman, found that when the sin of the
angle of incidence is divided by the sin of the angle of refraction, the
result is a constant value for a given interface (boundary layer between
specific materials). This constant number was named the Relative Refractive
Index and is specific for each pair of media. For an air-to-water interface,
the relative refractive index is 1.33.
A more useful quantity is the Absolute Refractive Index. This
is the relatve refractive index for a vacuum-to-medium interface and is
specific for each medium. Some examples are: Rock salt = 1.54,
Diamond = 2.42, Ethyl Alcohol = 1.36.
(Figures quoted from Eddy De Jong, 1991. Physics One,
Heinemannn Australia.)
Snell's Law
The relationship between the angles of incidence and refraction is now
known universally (except in France  )
as Snell's Law. See below.
)
as Snell's Law. See below.
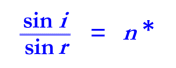 |
Where:
|
i is the angle of incidence
r is the angle of refraction
n* is the relative refractive index
for the 2 media involved |
Example:
A ray of light strikes an air-water interface
at an angle of 40 degrees from the normal. The relative refractive index
for the interface is 1.33. Find the angle of refraction.
Solution:
Substitute in given information
(i = 40, n* = 1.33)
Rearrange equation to get r on its own.
Turn both sides upside down to get rid of the reciprocal
Find sin 40 and calculate the value of sin r
Use the inverse sin button on your calculator to find the value for
r.
|
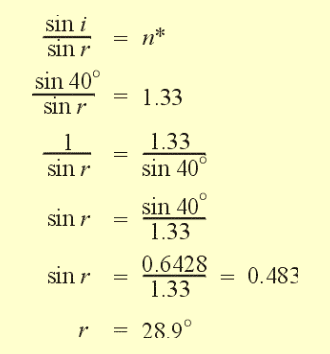 |